2023/11/25 公開
第2回講座でECの在庫管理入門で解説いたしましたが、もう一度、復習してみましょう。
という計算式となりますので、在庫日数(出荷対応に数)を算出するのにどうしても1日の需要予測数が必要となります。
需要予測の算出は、SCMの研究テーマとなっており、各社がいくつかの算出方法を研究・開発しております。
ここで重要なポイントで、確実な予測法は、存在しないということを押さえておきたいと思います。
どれだけお金をかけて、複雑なロジックで予測して、確実に当たるものではありません。
今では、流行のAIを利用したり、AIを含めたいくつかの予測を複合的に利用したりする予測法が報告されています。
この中で、最もベーシックな需要予測理論を今回、ご紹介させていただきます。
それは、移動平均法です。
なぜ、この理論かというと、AIなどを活用すると、予測値と実績値の乖離が出た場合、検証が非常にやりにくい点と、 初心者は、ベーシックな手法の理解が重要との考えによるものです。
しかしながら、この理論は、新製品の需要予測には不向きのため、そちらには、AIが向いているように思います。
今後、弊社の研究課題となると思います。
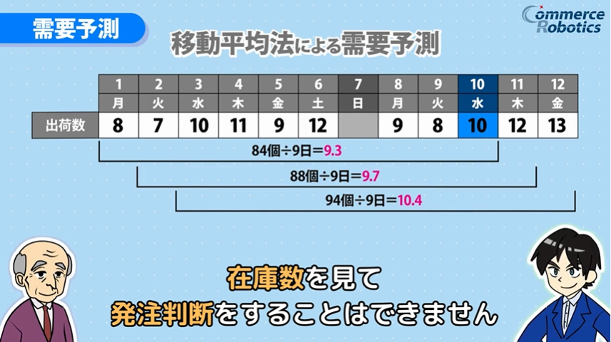
以下の図は、商品Aの出荷実績です。毎日、変動していることが分りますね。
また、7日は、休業日となっています。
この図では、9日間の移動平均値を毎日算出しています。
11日が9.3個、12日が9.7個、13日が10.4個 と 予測値も毎日変動しますね。
毎日、出荷が完了したら、過去9営業日の平均値を算出するのが移動平均法です。
毎日1日分移動するので、移動がつくと理解していただけると覚えやすいと思います。
在庫処分やB2B出荷など異常値は、計算から排除する必要があります。
需要予測が理解できたので、在庫日数(出荷対応日数)を算出してみましょう。
12日(金)の業務終了時点で6.7日分の在庫を所有していることが分りました。
この在庫日数は、毎日減って少なくなっていきます。
もうひとつ重要なものがL/T(リードタイム日数)です。
在庫日数(出荷対応日数)がL/Tよりも小さくなってしましったら、欠品となってしまうことが分ります。
12日(金)には、発注が必要であることが分ります。
| 日付 | 10 | 11 | 12 | 13 |
|---|---|---|---|---|
| 曜日 | 水 | 木 | 金 | 土 |
| 在庫数(開始) | 100 | 90 | 78 | 65 |
| 出荷数(当日) | 10 | 12 | 13 | |
| 在庫数(終了) | 90 | 78 | 65 | |
| 需要予測 | 9.3 | 9.7 | 10.4 | |
| 在庫日数 (出荷対応日数) |
8.4日 | 6.7日 | ||
| リードタイム日数 | 6日 | 6日 | 6日 | 6日 |
適正在庫の定義は、非常に難しいものとなります。
本来は、自社が自ら決めた在庫日数分の在庫量が適正在庫となります。
しかしながら、制約条件というものがあります。
最小発注量や最低発注金額などです。
それらの制約条件を加味して、持たざる得ない在庫量が「適正在庫量」と定義できます。
それでは、過剰在庫とはどのような状態でしょうか?
適正在庫量を超えたものが、過剰在庫量と定義できます。
いずれにしても、在庫管理において重要なのは、以下の2つです。
これらは、カート・モールやOMS、WMSで管理することは不可能であることが分ります。
在庫日数管理が可能なEOSこそ、今後のEC運営に必要不可欠なツールとなると思います。
次の講座では、適正在庫を管理する手法について解説いたします。